Power-and-Machines-notes/notes.md

Power types in motor

Type	Description	Equivalent terms
Input power	Power into machine. V_T=V_{3\phi}, I_L=I_{3\phi}	P_\text{in}, \sqrt{3}V_TI_L\cos(\theta)
Output power	Mechanical output power of the machine, excludes losses	P_\text{out}, P_\text{load}
Converted power	Total electrical power converted to mechanical power, includes useful power and mechanical losses inside machine	P_\text{conv}, P_\text{converted}, P_\text{mech}, P_\text{developed}, \tau_\text{mech}\times\omega_m
Airgap power	Power transmitted over airgap.	P_\text{AG}, \tau_\text{mech}\times\omega_s
Mechanical loss	Power lost to friction and windage	P_\text{mechanical loss}, P_\text{F\\\&W}, P_\text{friction and windage}
Core loss	Power lost in machine magnetic material due to hysteresis loss and eddy currents	P_\text{core}
Rotor copper loss	Due to resistance of rotor windings	P_r, P_\text{RCL}
Stator copper loss	Due to resistance of stator windings	P_s, P_\text{SCL}
Miscellaneous loss	Add 1% to losses to account for other unmeasured losses	P_\text{misc}, P_\text{stray}

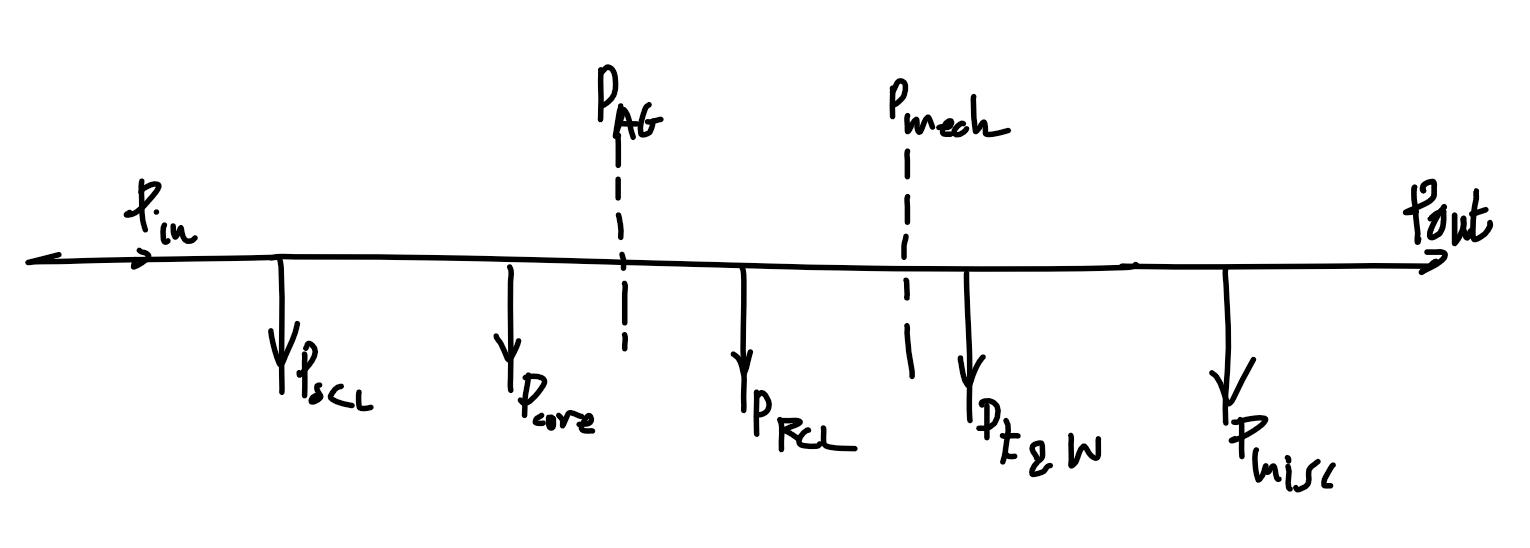
\begin{align}
P_\text{in}&=P_\text{SCL}+P_\text{RCL}+P_\text{core}+P_\text{F\\\&W}+P_\text{misc}+P_\text{out}\\
P_\text{AG}&=P_\text{RCL}+P_\text{F\\\&W}+P_\text{misc}+P_\text{out}\\
P_\text{mech}&=P_\text{F\\\&W}+P_\text{misc}+P_\text{out}
\end{align}

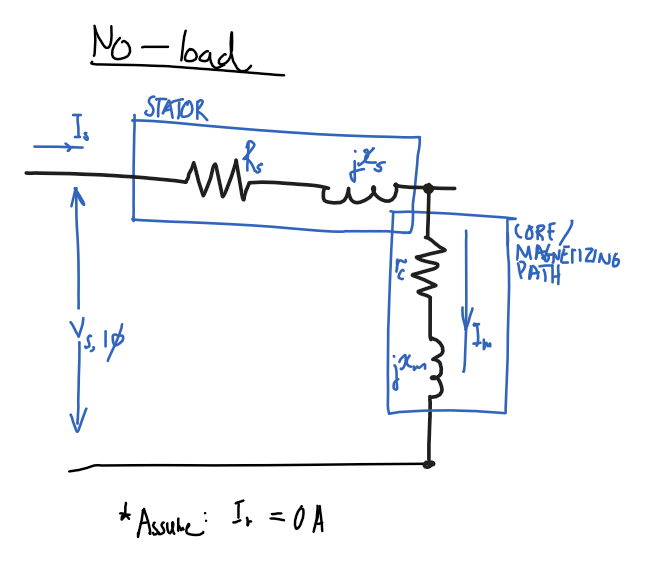
No-load test

Assumption	Eqn	Reason
rotor current is insignificant	I_r \approx 0	high rotor resistance
no output mechanical power	P_\text{out}=0	no load
high rotor resistance	R_r/s\to \infty	s\to 0, high slip at no load

Using assumptions, remove rotor part of circuit and only consider stator and magnetizing path.

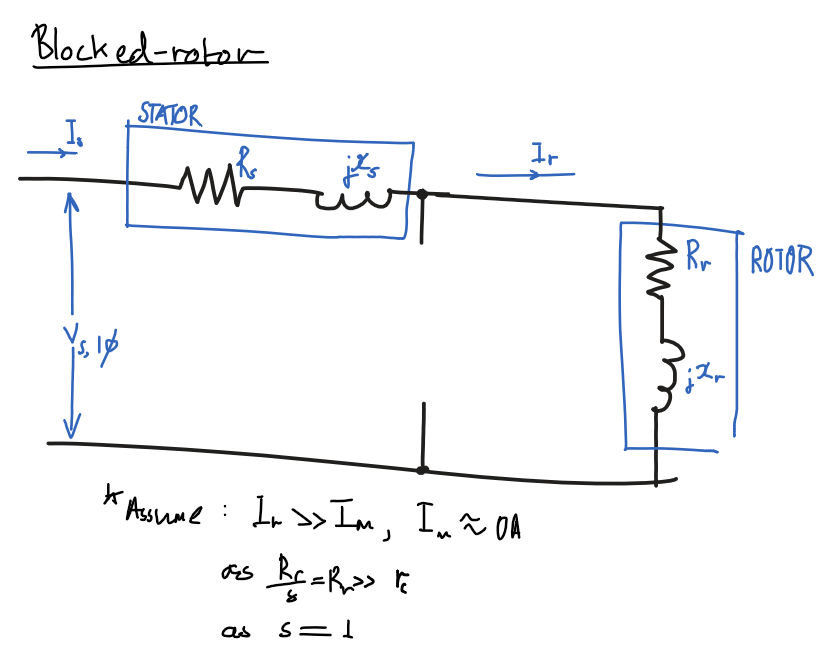
Blocked rotor test

Assumption	Eqn	Reason
ignore magnetizing path	I_r\ggg I_m	magnetizing current is low compared to rotor current as rotor resistance is low
low rotor resistance	R_r/s\approx R_r	s\approx 1, slip is 1 when blocked
	X_r\approx f_0/f_{BL}\times X_r'	X_r'\approx X_{BL}/2
	X_r'\approx X_{BL}/2	X_s\approx X_r'
	X_s\approx X_r'

Equivalent model

Assumption	Eqn	Reason
	x_m\approx X_m	R_c\ggg X_m\Rightarrow r_c\lll x_m
	r_c\approx {X_m}^2/R_c	R_c\ggg X_m\Rightarrow r_c\lll x_m