Power-and-Machines-notes/README.md

!\[\]\(([^\)]*)\)
<center><img src="$1" width=400px></center>

Why are the drawings bad?

I draw them with a mouse

Etc

FIRST-PASS CHECKS

• Double check all are in the correct phase! Multiplications and divisions by \sqrt{3} or 3 where necessary must be checked! Try annotating everything that does not have an associated phase.
• Check conjugate in current. \bar{S}=\bar{V}\bar{I}^*
• Check transformer parameters are referred to the proper side

Y-\Delta transformation (Balanced case)

Z_\Delta=3Z_Y

Types of power factors (From ENSC2003)

Where \bar{S}=|\bar{S}|\angle\varphi:

 \varphi = \arctan\left(\frac{Q}{P}\right) = \theta_v-\theta_i

	Lagging	Leading	Unity
Voltage	Current behind	Current ahead	In phase
Load type	Inductive	Capacitive	Resistive
Q	Q>0	Q<0	Q=0
\varphi	\varphi>0°	\varphi<0°	\varphi=0°
PF [Load]	[0,1)	[0,1)	1
PF [Source]	[0,-1)	[0,-1)	-1

Power types in induction motor

Type	Description	Equivalent terms
Input power	Power into machine. V_T=V_{3\phi}, I_L=I_{3\phi}	P_\text{in}, \sqrt{3}V_TI_L\cos(\theta)
Output power	Mechanical output power of the machine, excludes losses	P_\text{out}, P_\text{load}
Converted power	Total electrical power converted to mechanical power, includes useful power and mechanical losses inside machine	P_\text{conv}, P_\text{converted}, P_\text{mech}, P_\text{developed}, \tau_\text{mech}\times\omega_m
Airgap power	Power transmitted over airgap.	P_\text{AG}, \tau_\text{mech}\times\omega_s
Mechanical loss	Power lost to friction and windage	P_\text{mechanical loss}, P_\text{F\\\&W}, P_\text{friction and windage}
Core loss	Power lost in machine magnetic material due to hysteresis loss and eddy currents	P_\text{core}
Rotor copper loss	Due to resistance of rotor windings	P_r, P_\text{RCL}
Stator copper loss	Due to resistance of stator windings	P_s, P_\text{SCL}
Miscellaneous loss	Add 1% to losses to account for other unmeasured losses	P_\text{misc}, P_\text{stray}

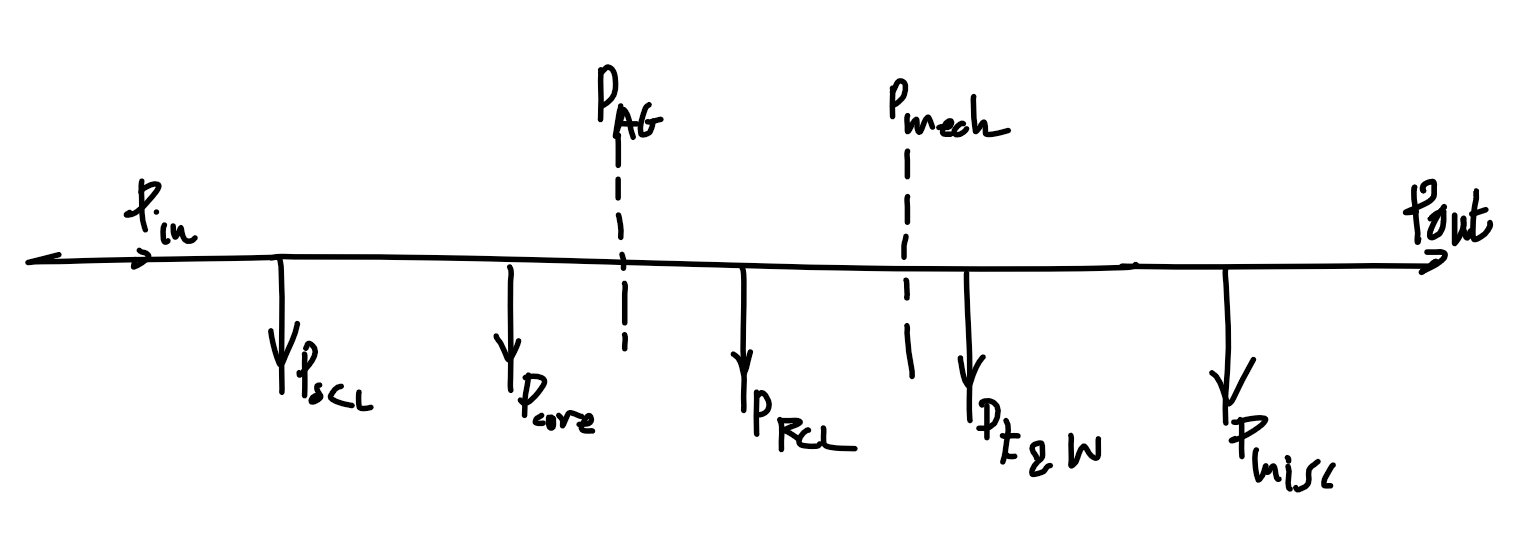
\begin{align}
P_\text{in}&=P_\text{SCL}+P_\text{RCL}+P_\text{core}+P_\text{F\\\&W}+P_\text{misc}+P_\text{out}\\
P_\text{AG}&=P_\text{RCL}+P_\text{F\\\&W}+P_\text{misc}+P_\text{out}\\
P_\text{mech}&=P_\text{F\\\&W}+P_\text{misc}+P_\text{out}
\end{align}

Note - assume loss is 0 if not mentioned!

Type	Description	Symbols
Load torque, Shaft torque	Torque experienced by load after all losses	\tau_\text{load}, \tau_\text{shaft}

3\phi induction motor

Etc.

• Slip speed N_\text{slip}=N_{s\text{ (sync)}}-N_r=sN_{s\text{ (sync)}}

• "1/4 of rated load" != "1/4 times full load"

  • Means 1/4 of full load slip as it is in the linear region. Accounts for the minimum load.

• Rated power stated in machine specification refers to the output power P_\text{out}, and excludes all losses.

• Speed regulation using machine speed: $$\text{SR}=\frac{N_{r,\text{NL}}-N_{r,\text{FL}}}{N_{r,\text{FL}}}

Diagram

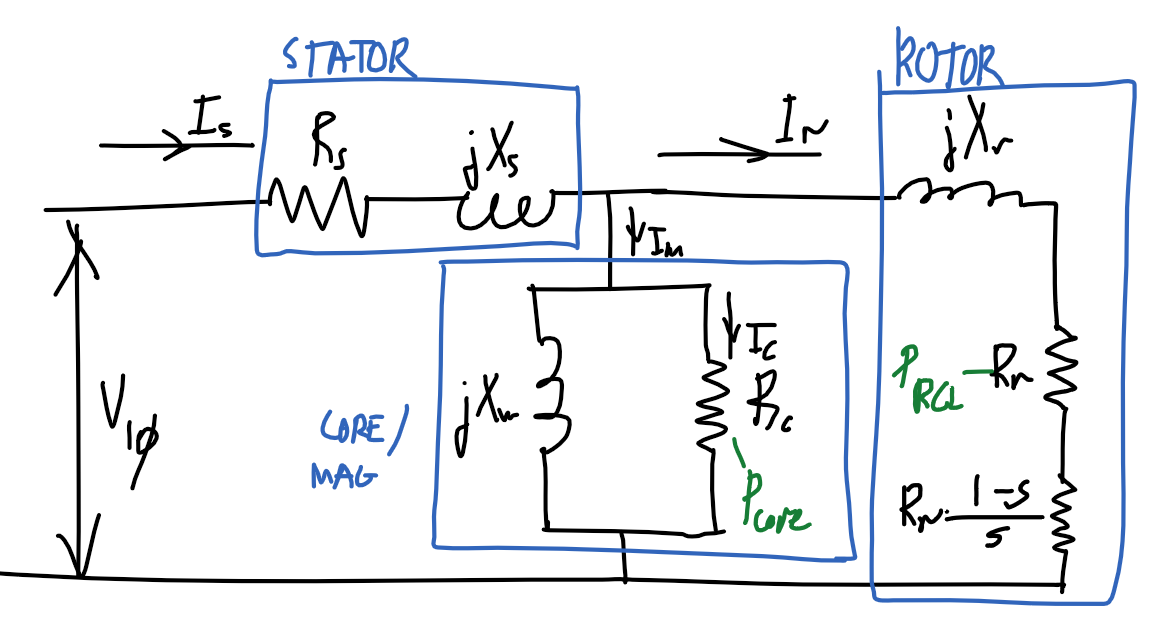
Equivalent model

Assumptions

• x_m\approx X_m
  • R_c\ggg X_m\Rightarrow r_c\lll x_m
  • x_m=\frac{{R_c}^2}{{R_c}^2+{X_m}^2}X_m\approx\frac{\cancel{{R_c}^2}}{\cancel{{R_c}^2}}X_m=X_m
• r_c\approx {X_m}^2/R_c
  • R_c\ggg X_m\Rightarrow r_c\lll x_m
  • r_c=\frac{{X_m}^2}{{R_c}^2+{X_m}^2}R_c\approx\frac{{X_m}^2}{{R_c}^2}R_c=\frac{{X_m}^2}{R_c}

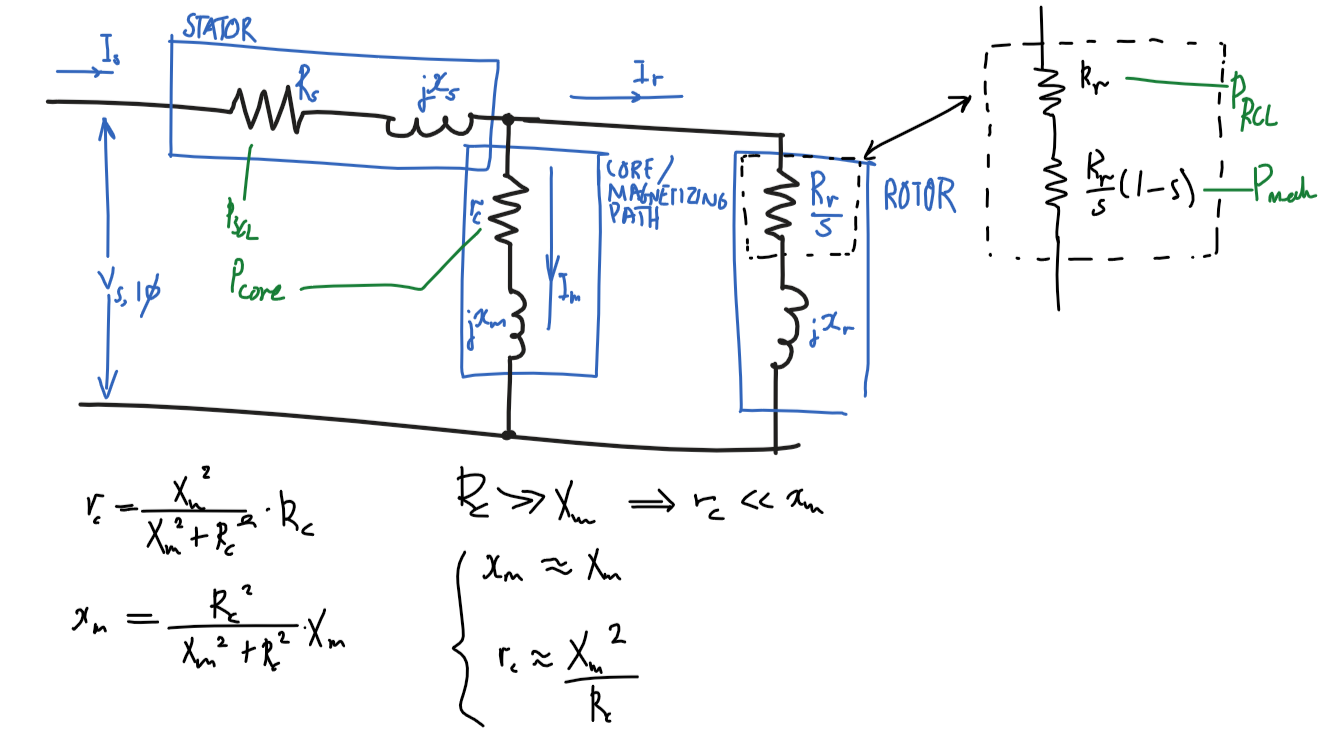
Diagram

DC test

\Delta machine

R_s=\frac{3}{2}\cdot\frac{V_{\text{DC},3\phi}}{I_{\text{DC},3\phi}}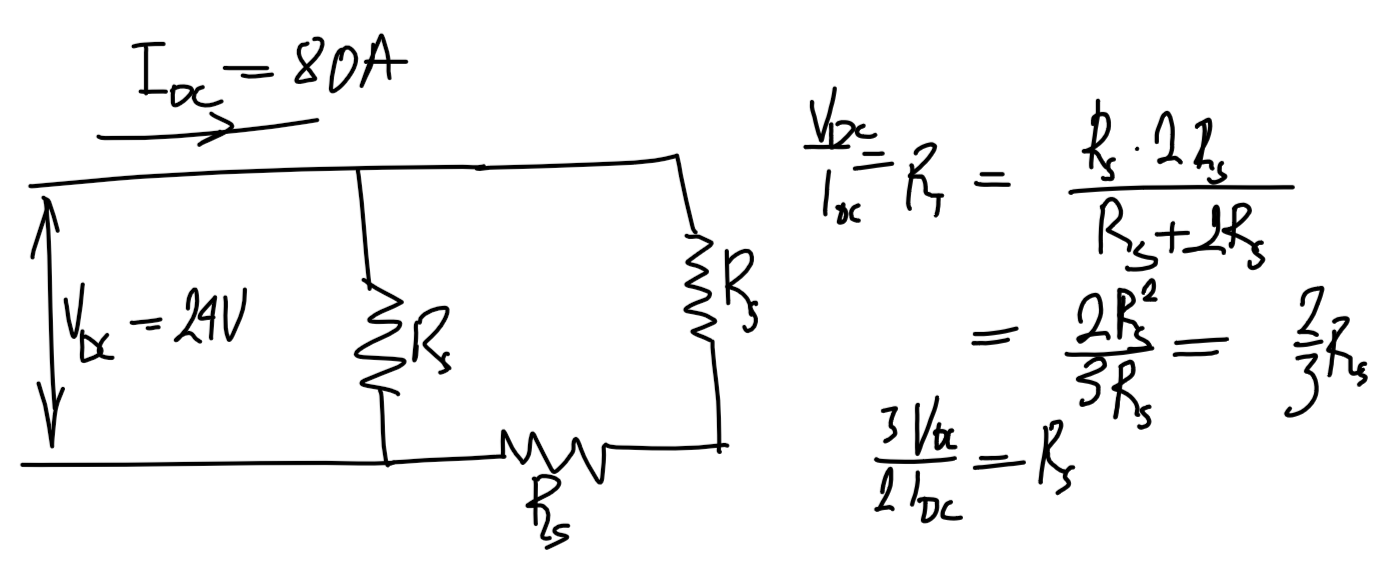

Y machine

R_s=\frac{1}{2}\cdot\frac{V_{\text{DC},3\phi}}{I_{\text{DC},3\phi}}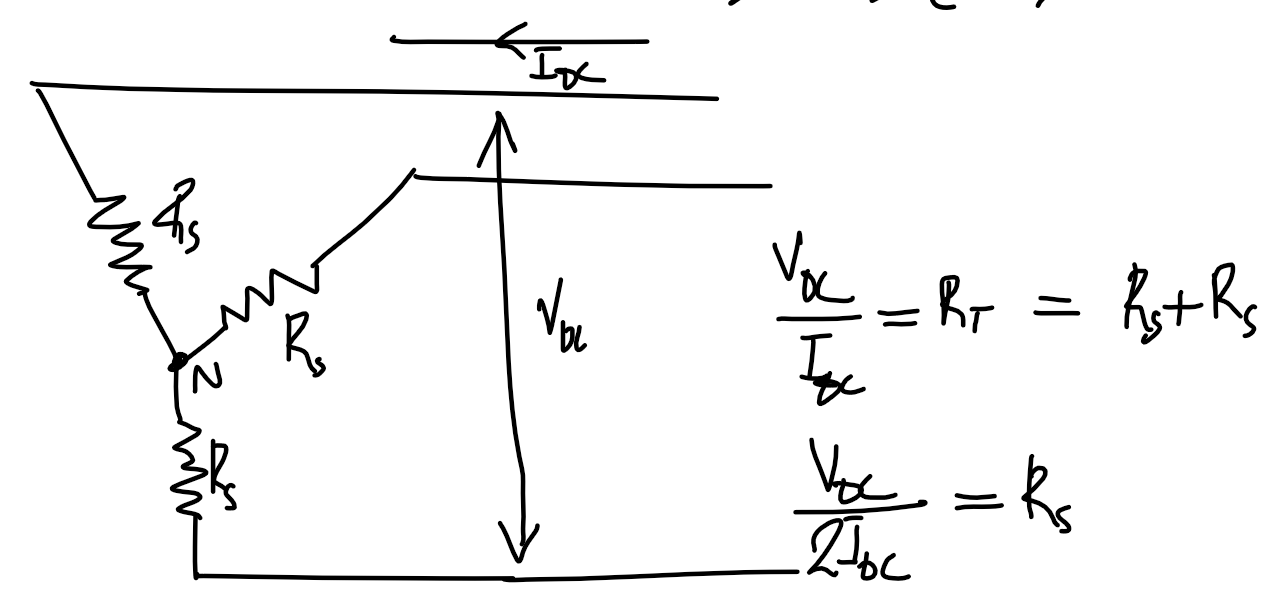

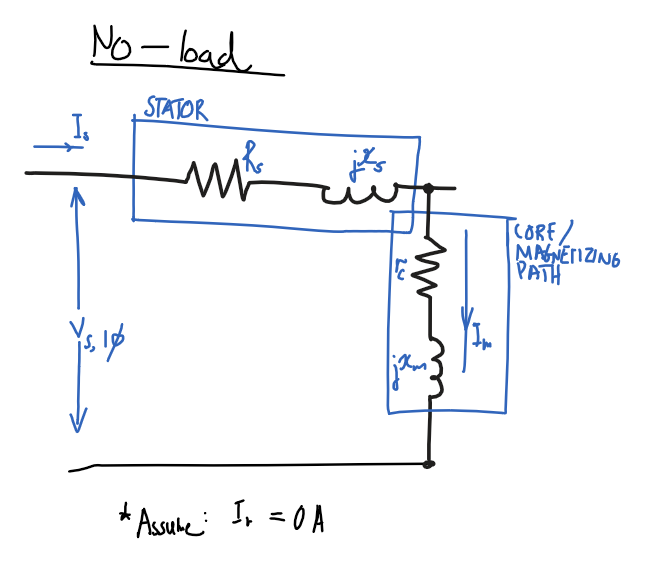
No-load test

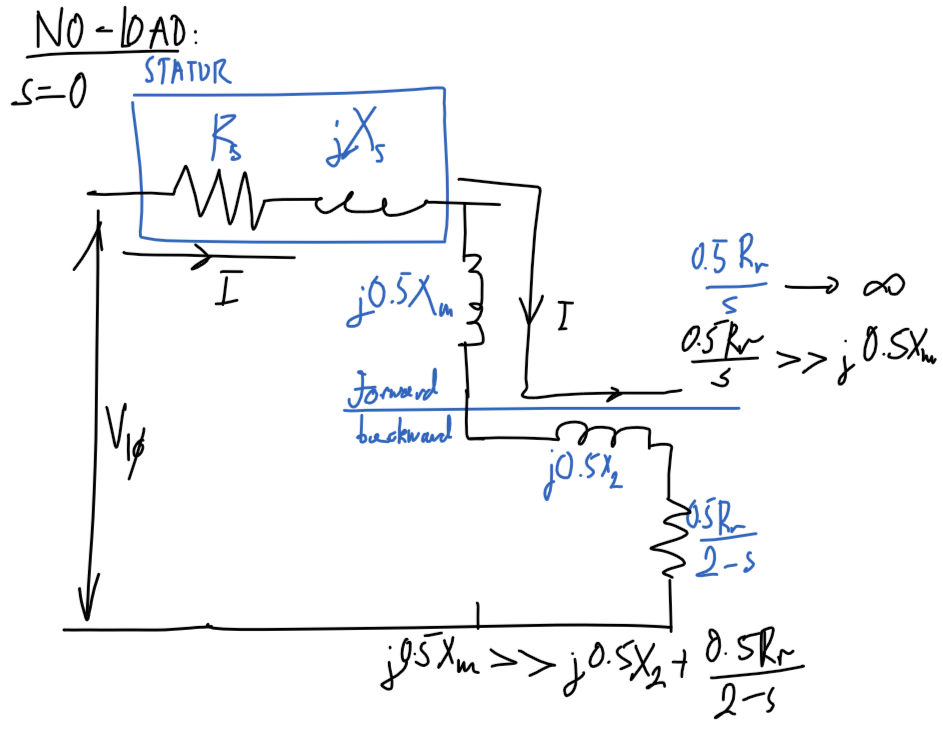
Assumptions

• P_\text{out}=0
  • No output power as no load.
• R_r/s=\infty and I_r=0
  • Infinite rotor resistance, ignore rotor path.

Diagram

Using assumptions, remove rotor part of circuit and only consider stator and magnetizing path.

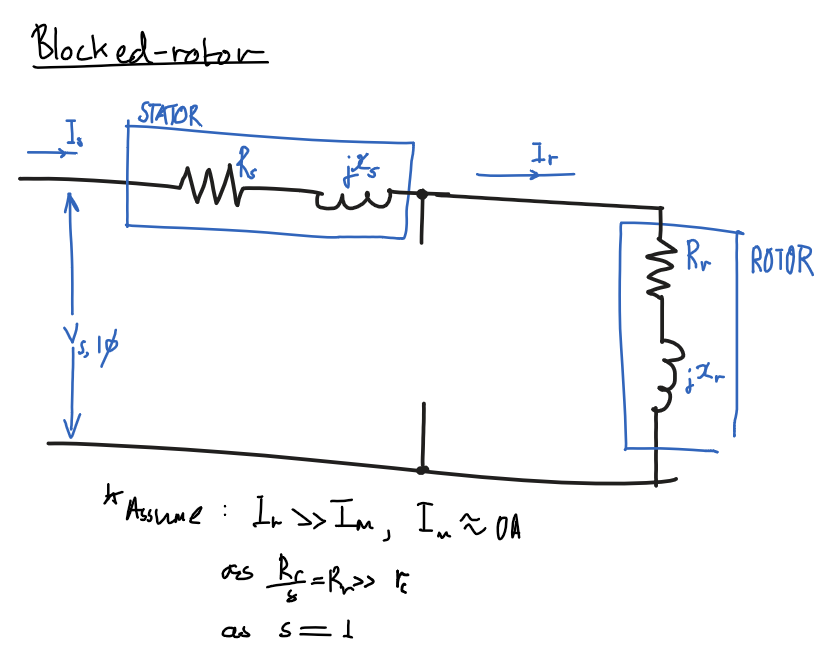
Blocked rotor test

Assumptions

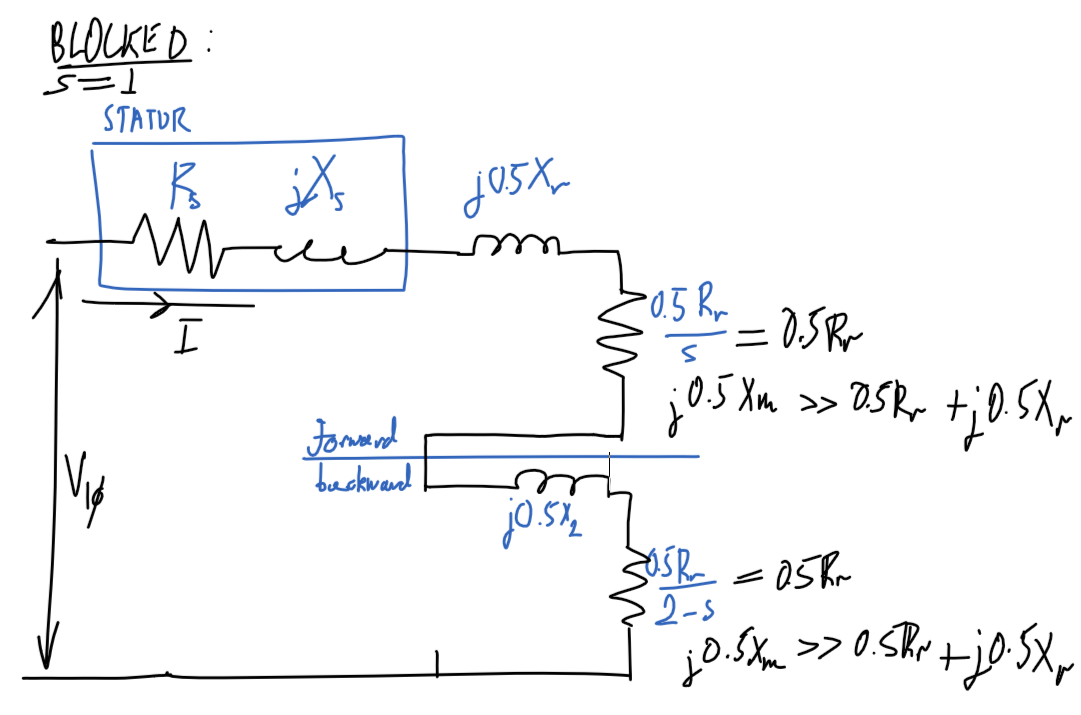
• Ignore magnetizing path, I_m=0
  • I_r\ggg I_m as R_r/s\ggg Z_m
• R_r/s=R_r, s=1
  • Slip is 1 as rotor is blocked.
• x_s=x_r'
  • Same number of turns in stator and rotor
• and x_r=f_0/f_\text{BL} \times x_r'
  • Note: x_r' is the inductance at f_\text{BL}, the blocked rotor test frequency which is less than the nominal frequency f_0

Diagram

Ignore magnetizing path

---

Single-phase induction motor

Diagram

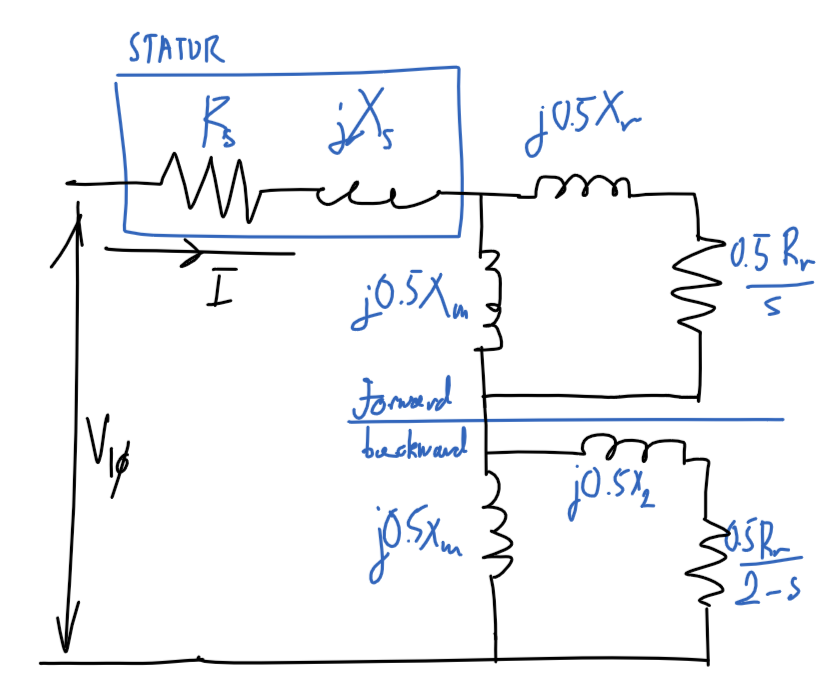
Blocked-rotor

Diagram

No-load

Diagram

Synchronous machine

Etc

E_A=V_{1\phi}-I_A(R_A+j X_s)

I_A=\text{CONJUGATE}\left(\frac{|S_{3\phi}|\angle\arccos(x)}{3V_{1\phi}}\right), \begin{cases}x=+\text{PF} && \text{lagging} \\ x=-\text{PF} && \text{leading}\end{cases}

Voltage regulation

\text{VR}=\frac{|V_\text{NL}|-|V_\text{FL}|}{|V_\text{FL}|}=\frac{|E_A|-|V_{1\phi,\text{rated}}|}{|V_{1\phi,\text{rated}}|}

• V_\text{FL} is the full-load voltage which is the full-load/maximum rated voltage at the output terminal.
• Calculate E_A at full load by calculating the current as shown above.
• V_\text{NL} is the no-load voltage, which in the no-load case will be E_A.

No-load	Full-load

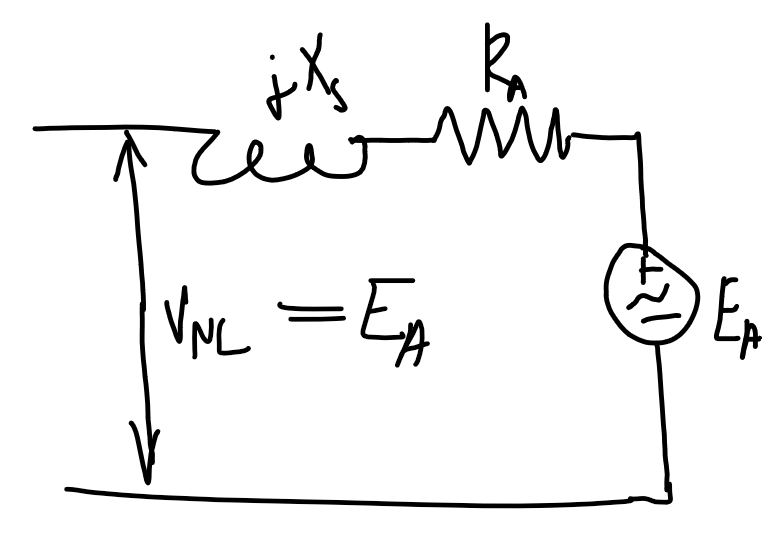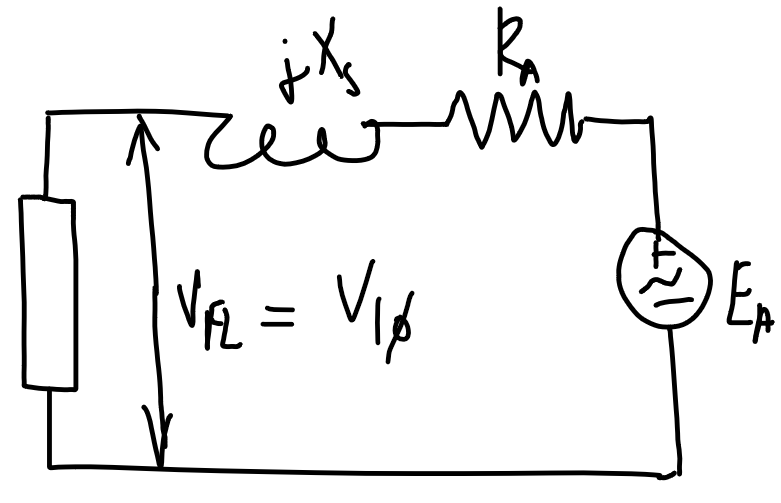Power factor	Voltage regulation
Lagging	Positive
Unity	Near 0
Leading	Negative

Open and short circuit test

Note - double-check if the axis refers to per-phase or line voltage/current.

Open-circuit test	Short-circuit test

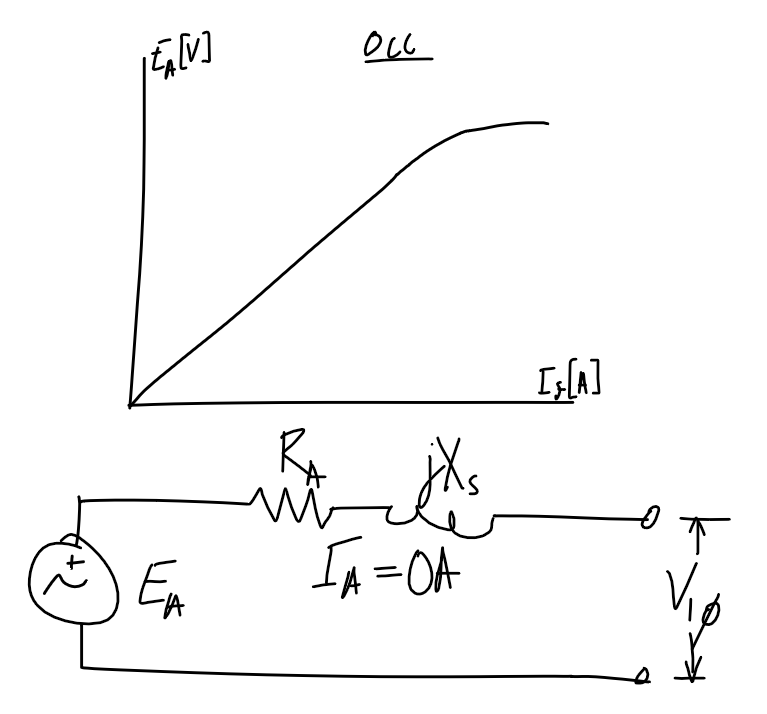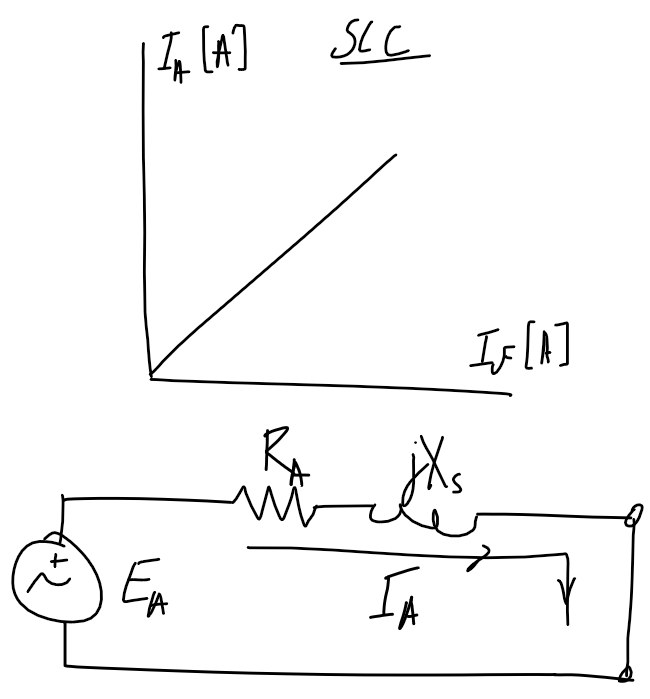Power flow

P_\text{out} is the rated power

P_\text{out}=S_\text{rated}\times \text{PF}

\begin{align}
P_\text{in}&=P_\text{copper}+P_\text{core}+P_\text{F\\\&W}+P_\text{misc}+P_\text{out}\\
P_\text{mech}&=P_\text{F\\\&W}+P_\text{misc}+P_\text{out}
\end{align}

---

Magnetic circuit analogy

Magnetic circuit	name		Electrical circuit	name
$$\mathcal F$$	Magnetomotive force [A-turn]		$$\mathcal E$$	Electromotive force [V]
$$\mathcal R$$	Reluctance [1/H]		$$R$$	Resistance [$\Omega$]
$$\Phi$$	Magnetic flux [Wb]		$$I$$	Current [A]
$$\mathcal P=\frac{1}{\mathcal R}	Permeance [H]		$$G=\frac{1}{R}	Conductivity [$\mho$]
$$\mathcal F=\Phi\mathcal R$$	Hopkinson's law		$$V=IR$$	Ohm's law
$$\mathcal R=\frac{l}{\mu A}			$$R=\frac{l}{\sigma A}

---

Transformers

Z_P=Z_S\left(\frac{N_P}{N_S}\right)^2=Z_S n^2

Maximum power.

If load is resistive ($jX_\text{load}=0$) then for maximum power transfer:

R_\text{load}=|{R_\text{src}}^2+j{X_\text{src}}^2|

Parameter identification

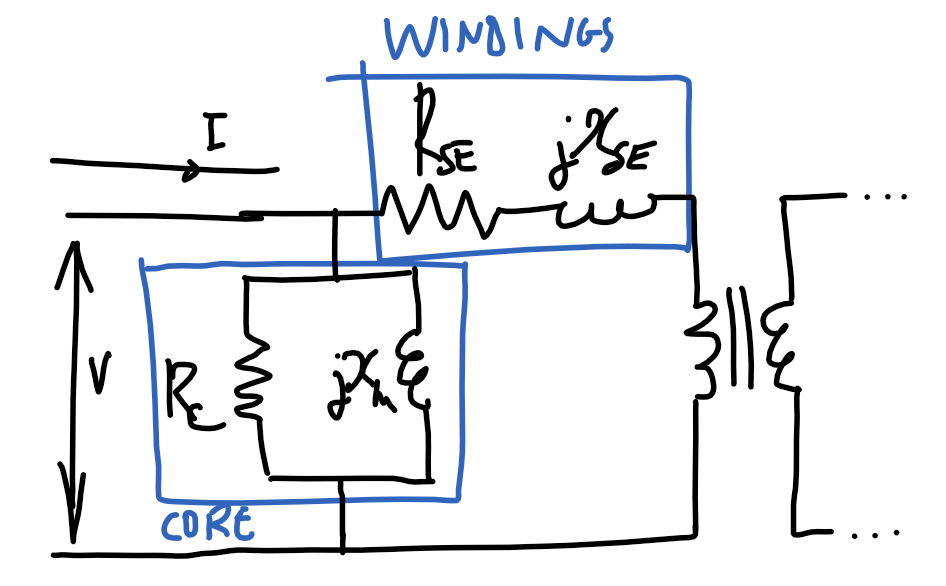
Open-circuit test	Short-circuit test

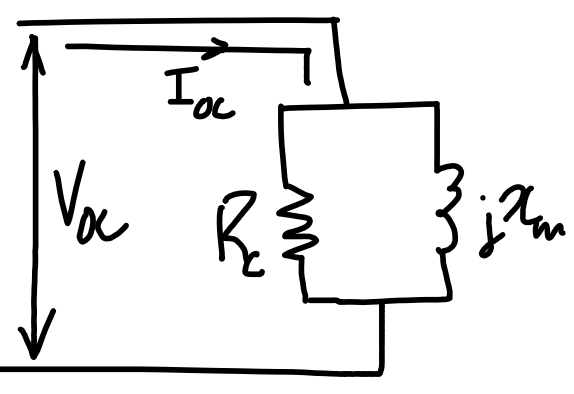Voltage regulation

\text{VR}=\frac{|V_\text{NL,P}|-|V_\text{rated,P}|}{|V_\text{rated,P}|}=\frac{|V_\text{in}|-|V_\text{rated,P}|}{|V_\text{rated,P}|}

Ignore shunt resistance. Refer from primary side. Use KVL to determine V_\text{in}.

Voltage regulation is typically small.

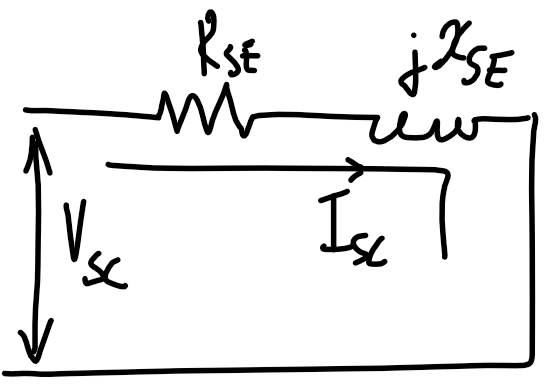
|V_\text{in}|=|V_\text{rated,P}+I_\text{L,P}\cdot\bar Z|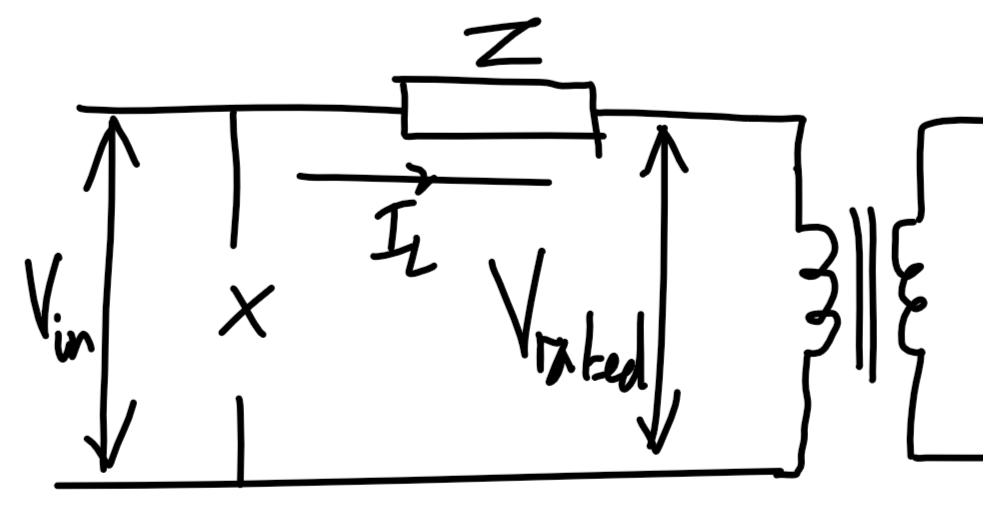

DC machine

Separately excited machine	Shunt excited	Series excited
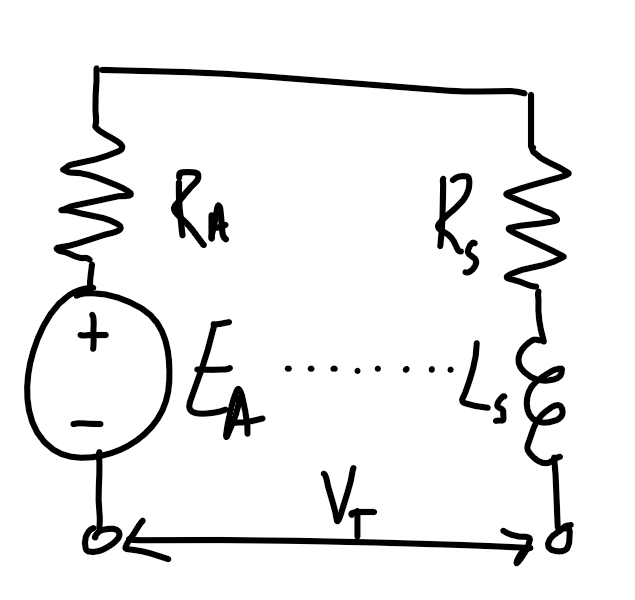	Similar torque-speed characteristic to separately-excited machine	High torque per ampere. Used in high-torque applications
Requires two independent voltage sources		Do not run unloaded - infinite speed at 0 torque as \omega\propto 1/\sqrt{\tau}
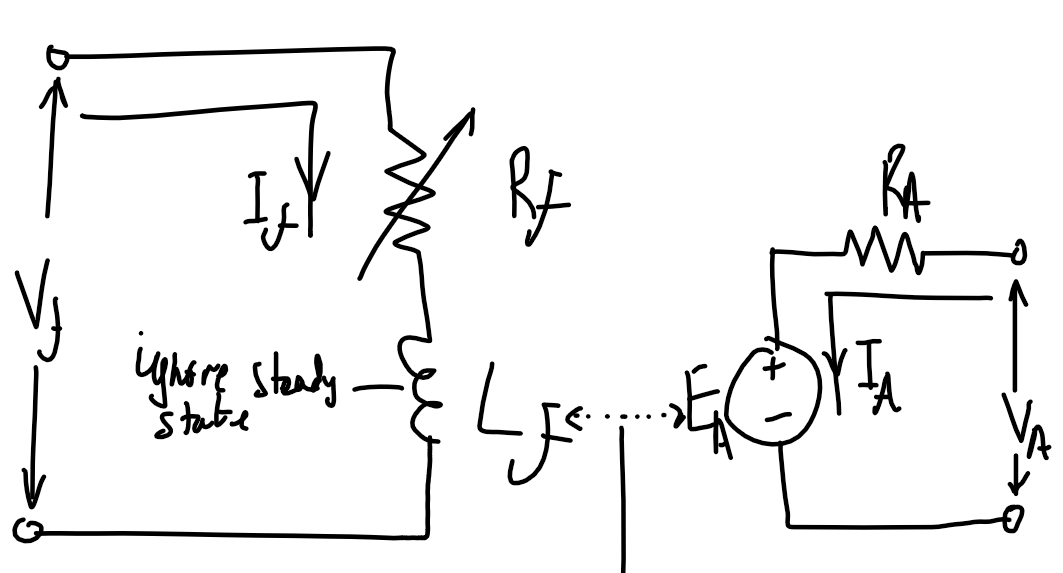
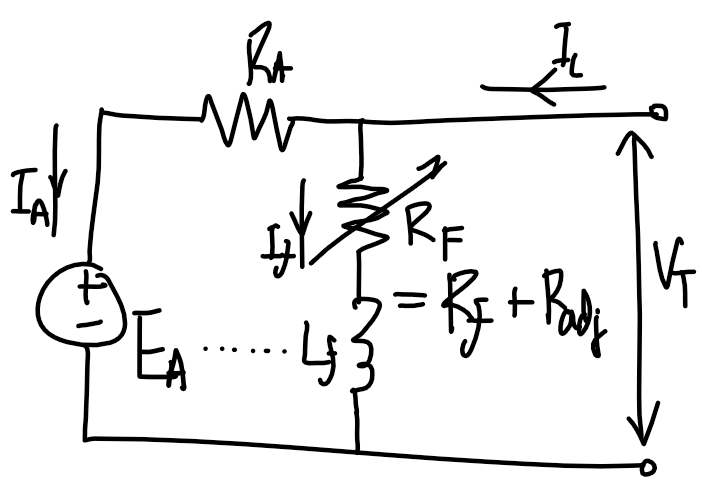
Motor control using R_f	Motor control using R_F	Motor control using V_T.

Starting DC motors

R_A might need to be adjusted so it is high initially in large DC motors, as the starting current is high since there is no back-emf created by E_A.

Magnetizating curve

When a question specifies the field current or R_\text{adj}, refer to magnetization curve. Magnetizating curve is valid at a specific speed n_{m1}, and the curve is used to find E_{A1}. Using the load condition to find the armature current I_A=\tau_\text{ind}/(K\varPhi), V_A can be used to find a second induced EMF E_{A2}. Using E_{A2} find the speed n_{m2} by scaling n_{m1} by E_{A2}/E_{A1}.

Idk

P_\text{mech}=E_AI_A

No-load separately excited machine. Assuming no mechanical losses.

E_A=V_A\text{ (No load)}

I_A=0\text{ (No load)}

Armature reaction causes increase in speed and causes instability as the core saturates near the poles. Can be reduced with compensating winding which is in series with the armature coil.

K\Phi\omega=E_A

K\Phi I_A=\tau

For shunt motor

K\Phi=\frac{V_T-R_AI_A}{\omega}

\tau=K\Phi I_A=\frac{V_T-R_AI_A}{\omega}I_A

Assume no saturation, speed locked(?):

This doesn't seem right. We are meant to use the machine constant and the proportionality of current to magnetic flux.

\frac{E_{A2}}{E_{A1}}=\frac{I_{f2}}{I_{f1}}