Power-and-Machines-notes/README.md

Why are the drawings bad?

I draw them with a mouse

Etc

FIRST-PASS CHECKS

• Double check all are in the correct phase! Multiplications and divisions by \sqrt{3} or 3 where necessary must be checked! Try annotating everything that does not have an associated phase.
• Check conjugate in current. \bar{S}=\bar{V}\bar{I}^*

Y-\Delta transformation (Balanced case)

Z_\Delta=3Z_Y

Types of power factors (From ENSC2003)

Where \bar{S}=|\bar{S}|\angle\varphi:

 \varphi = \arctan\left(\frac{Q}{P}\right) = \theta_v-\theta_i

	Lagging	Leading	Unity
Voltage	Current behind	Current ahead	In phase
Load type	Inductive	Capacitive	Resistive
Q	Q>0	Q<0	Q=0
\varphi	\varphi>0°	\varphi<0°	\varphi=0°
PF [Load]	[0,1)	[0,1)	1
PF [Source]	[0,-1)	[0,-1)	-1

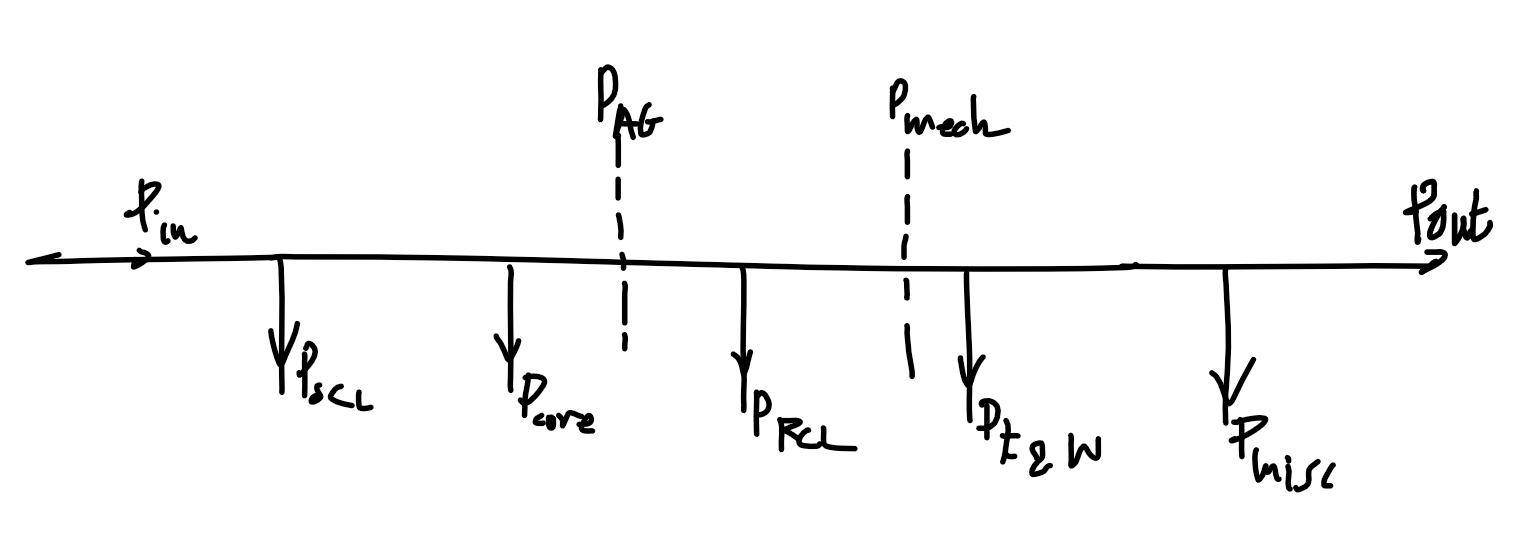
Power types in induction motor

Type	Description	Equivalent terms
Input power	Power into machine. V_T=V_{3\phi}, I_L=I_{3\phi}	P_\text{in}, \sqrt{3}V_TI_L\cos(\theta)
Output power	Mechanical output power of the machine, excludes losses	P_\text{out}, P_\text{load}
Converted power	Total electrical power converted to mechanical power, includes useful power and mechanical losses inside machine	P_\text{conv}, P_\text{converted}, P_\text{mech}, P_\text{developed}, \tau_\text{mech}\times\omega_m
Airgap power	Power transmitted over airgap.	P_\text{AG}, \tau_\text{mech}\times\omega_s
Mechanical loss	Power lost to friction and windage	P_\text{mechanical loss}, P_\text{F\\\&W}, P_\text{friction and windage}
Core loss	Power lost in machine magnetic material due to hysteresis loss and eddy currents	P_\text{core}
Rotor copper loss	Due to resistance of rotor windings	P_r, P_\text{RCL}
Stator copper loss	Due to resistance of stator windings	P_s, P_\text{SCL}
Miscellaneous loss	Add 1% to losses to account for other unmeasured losses	P_\text{misc}, P_\text{stray}

\begin{align}
P_\text{in}&=P_\text{SCL}+P_\text{RCL}+P_\text{core}+P_\text{F\\\&W}+P_\text{misc}+P_\text{out}\\
P_\text{AG}&=P_\text{RCL}+P_\text{F\\\&W}+P_\text{misc}+P_\text{out}\\
P_\text{mech}&=P_\text{F\\\&W}+P_\text{misc}+P_\text{out}
\end{align}

Note - assume loss is 0 if not mentioned!

Type	Description	Symbols
Load torque, Shaft torque	Torque experienced by load after all losses	\tau_\text{load}, \tau_\text{shaft}

3\phi induction motor

Etc.

• Slip speed N_\text{slip}=N_{s\text{ (sync)}}-N_r=sN_{s\text{ (sync)}}

• "1/4 of rated load" != "1/4 times full load"

  • Means 1/4 of full load slip as it is in the linear region. Accounts for the minimum load.

• Rated power stated in machine specification refers to the output power P_\text{out}, and excludes all losses.

• Speed regulation using machine speed: $$\text{SR}=\frac{N_{r,\text{NL}}-N_{r,\text{FL}}}{N_{r,\text{FL}}}

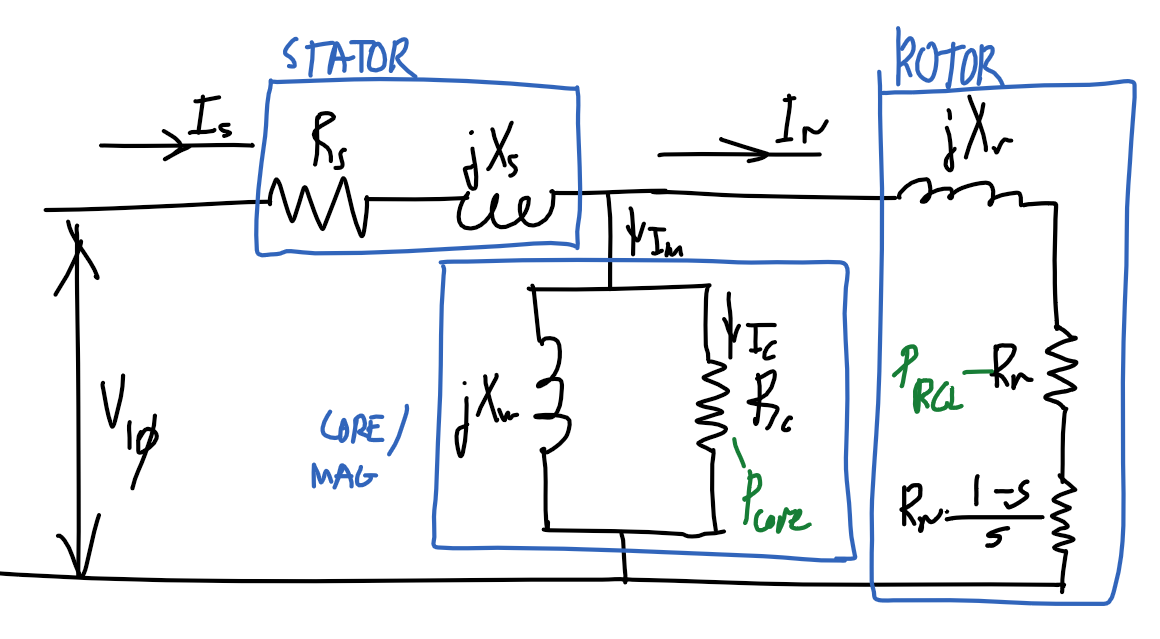
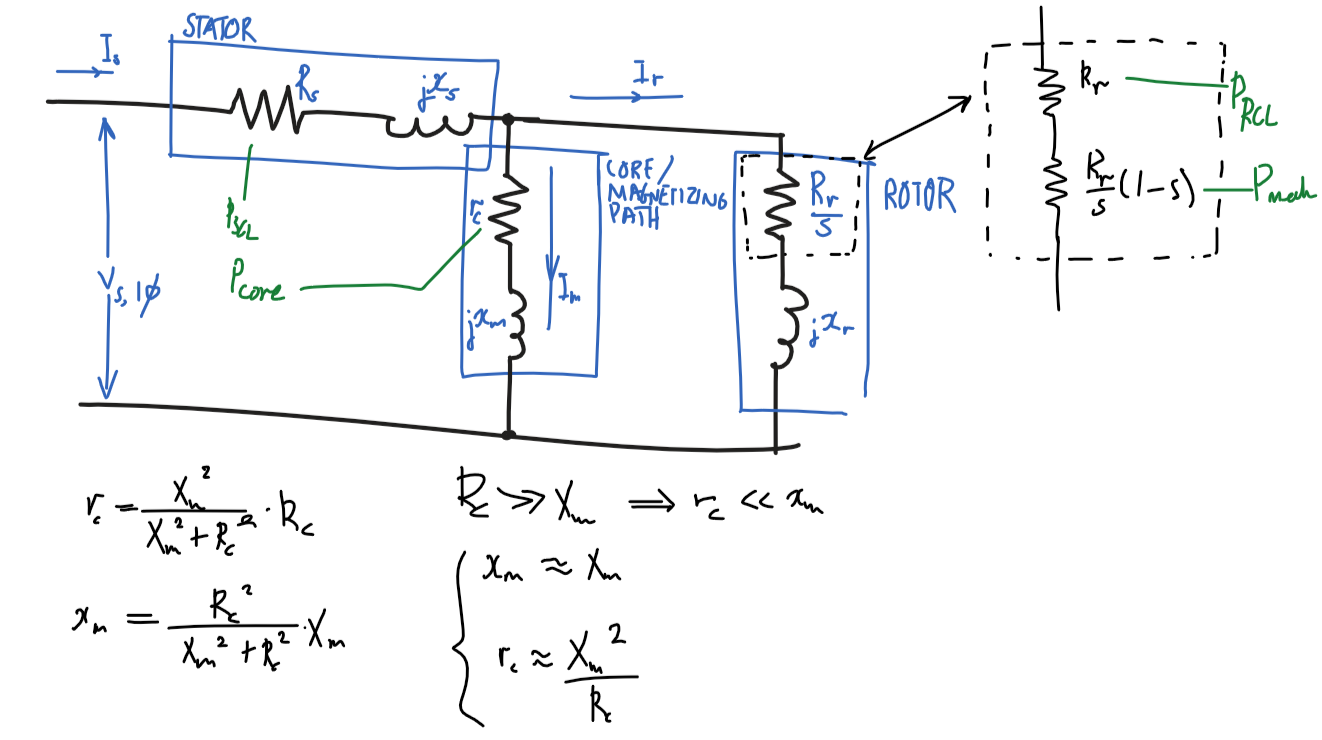
Diagram

Equivalent model

Assumptions

• x_m\approx X_m
  • R_c\ggg X_m\Rightarrow r_c\lll x_m
  • x_m=\frac{{R_c}^2}{{R_c}^2+{X_m}^2}X_m\approx\frac{\cancel{{R_c}^2}}{\cancel{{R_c}^2}}X_m=X_m
• r_c\approx {X_m}^2/R_c
  • R_c\ggg X_m\Rightarrow r_c\lll x_m
  • r_c=\frac{{X_m}^2}{{R_c}^2+{X_m}^2}R_c\approx\frac{{X_m}^2}{{R_c}^2}R_c=\frac{{X_m}^2}{R_c}

Diagram

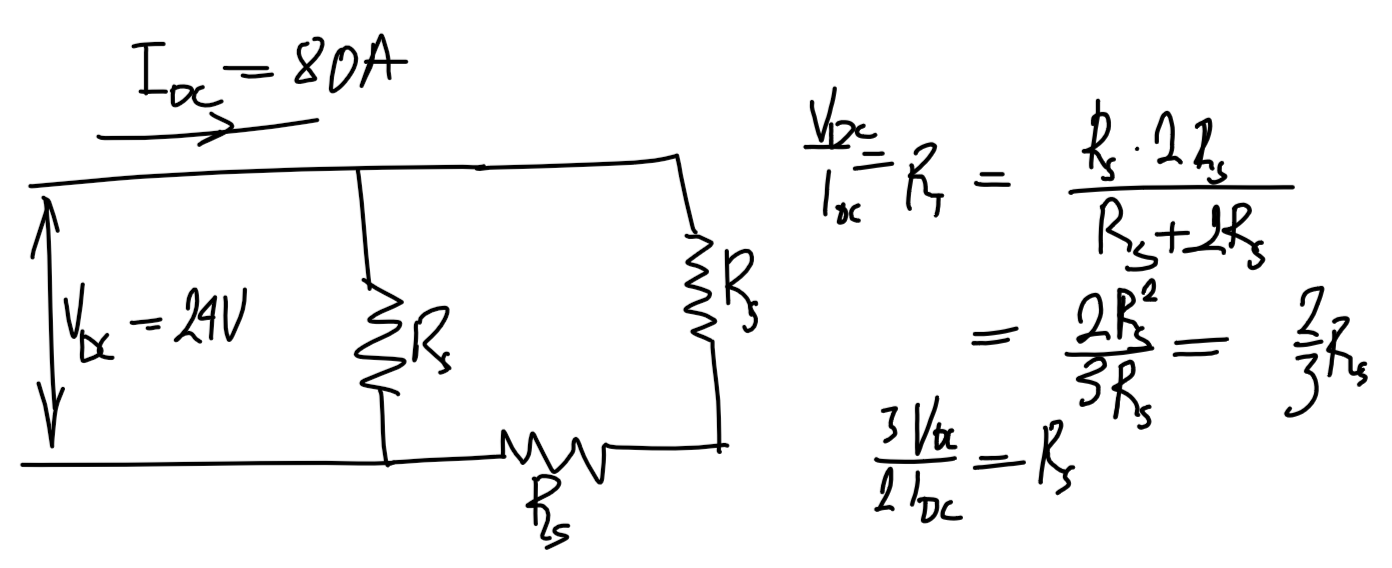
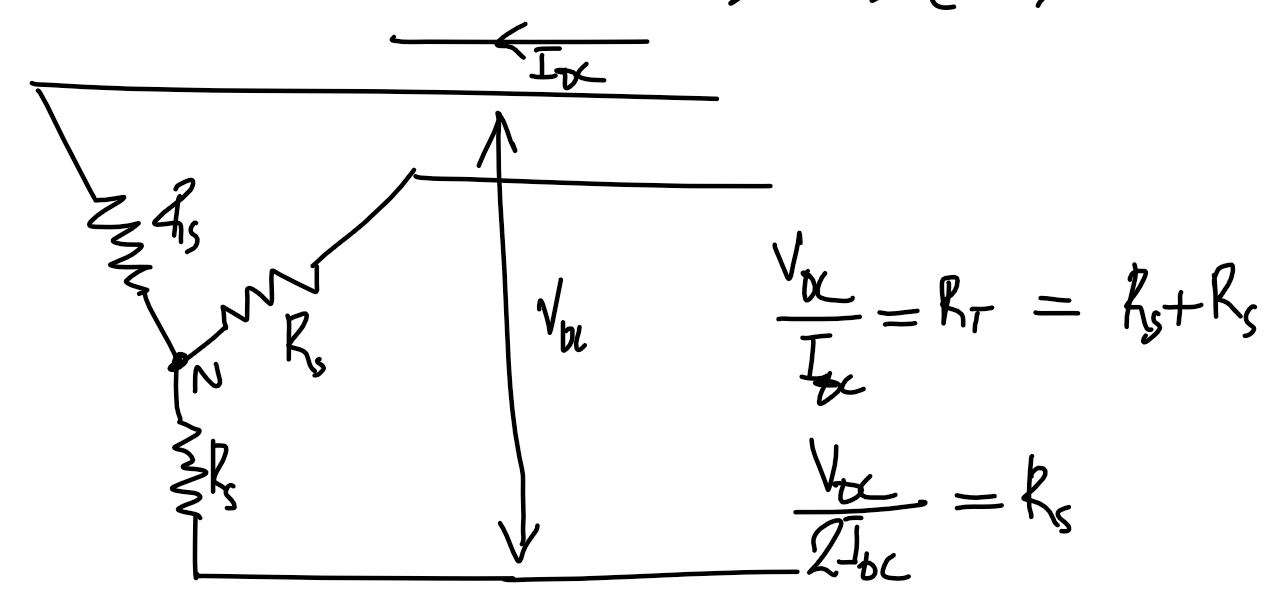
DC test

\Delta machine

R_s=\frac{3}{2}\cdot\frac{V_{\text{DC},3\phi}}{I_{\text{DC},3\phi}}

Y machine

R_s=\frac{1}{2}\cdot\frac{V_{\text{DC},3\phi}}{I_{\text{DC},3\phi}}

No-load test

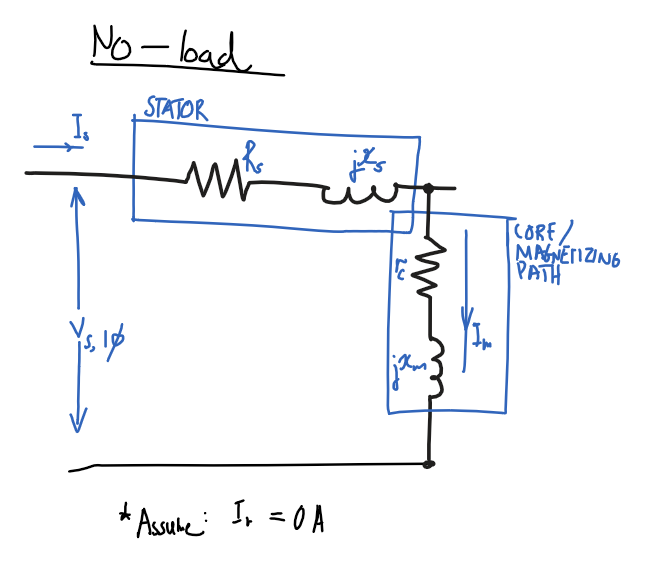
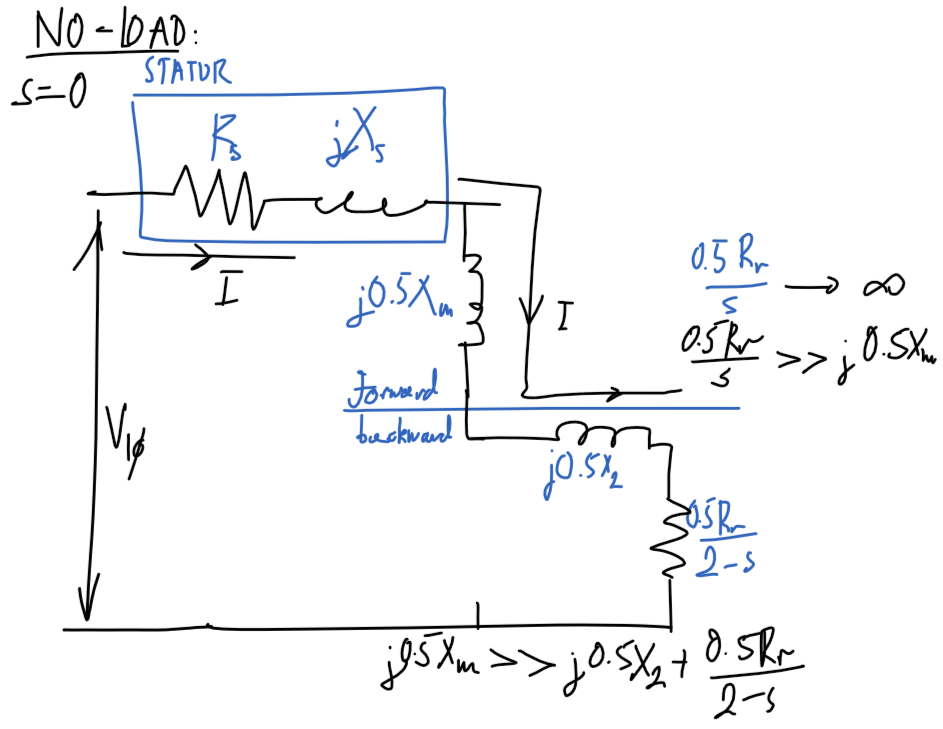
Assumptions

• P_\text{out}=0
  • No output power as no load.
• R_r/s=\infty and I_r=0
  • Infinite rotor resistance, ignore rotor path.

Diagram

Using assumptions, remove rotor part of circuit and only consider stator and magnetizing path.

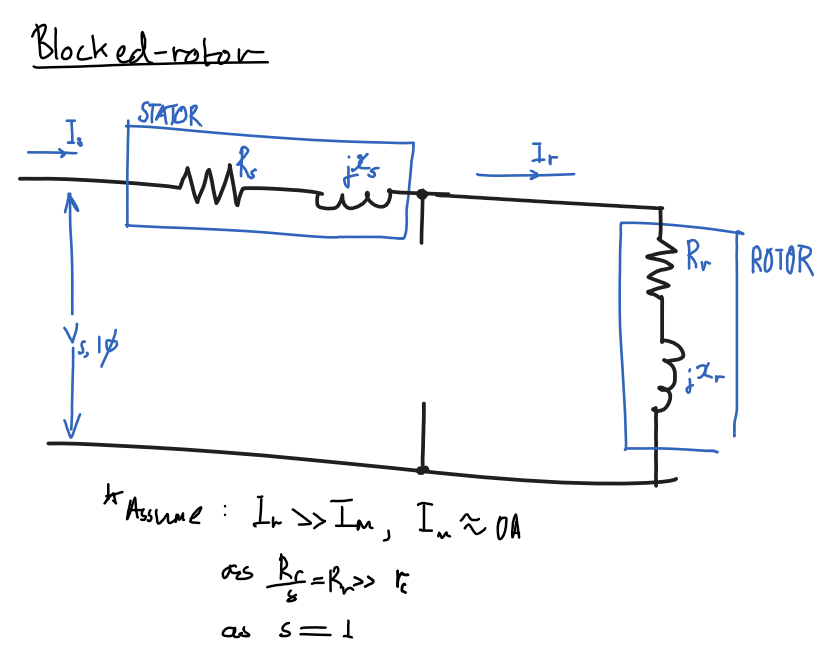
Blocked rotor test

Assumptions

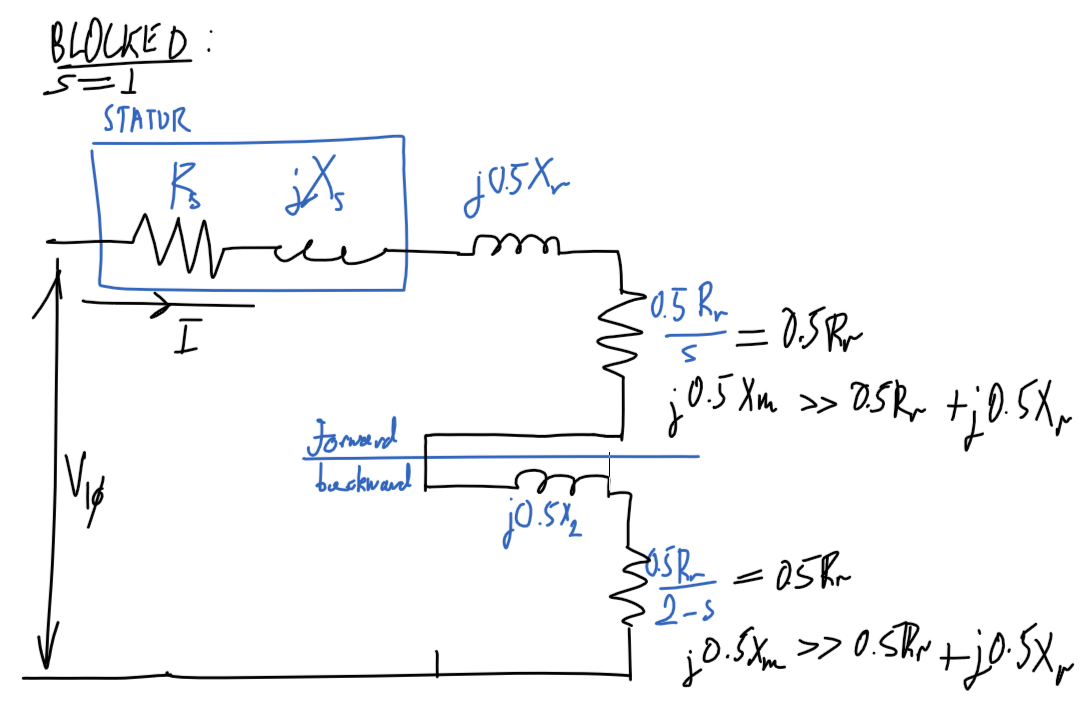
• Ignore magnetizing path, I_m=0
  • I_r\ggg I_m as R_r/s\ggg Z_m
• R_r/s=R_r, s=1
  • Slip is 1 as rotor is blocked.
• x_s=x_r'
  • Same number of turns in stator and rotor
• and x_r=f_0/f_\text{BL} \times x_r'
  • Note: x_r' is the inductance at f_\text{BL}, the blocked rotor test frequency which is less than the nominal frequency f_0

Diagram

Ignore magnetizing path

---

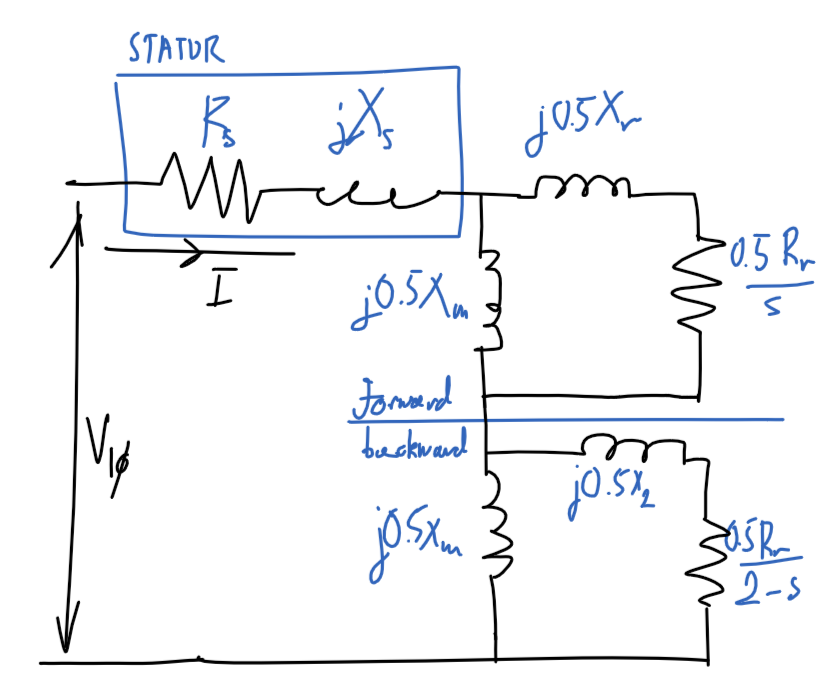
Single-phase induction motor

Diagram

Blocked-rotor

Diagram

No-load

Diagram

Synchronous machine

Etc

E_A=V_{1\phi}-I_A(R_A+j X_s)

I_A=\text{CONJUGATE}\left(\frac{|S_{3\phi}|\angle\arccos(x)}{3V_{1\phi}}\right), \begin{cases}x=+\text{PF} && \text{lagging} \\ x=-\text{PF} && \text{leading}\end{cases}

Voltage regulation

\text{VR}=\frac{|V_\text{NL}|-|V_\text{FL}|}{|V_\text{FL}|}=\frac{|E_A|-|V_{1\phi,\text{rated}}|}{|V_{1\phi,\text{rated}}|}

• V_\text{FL} is the full-load voltage which is the full-load/maximum rated voltage at the output terminal.
• Calculate E_A at full load by calculating the current as shown above.
• V_\text{NL} is the no-load voltage, which in the no-load case will be E_A.

No-load	Full-load

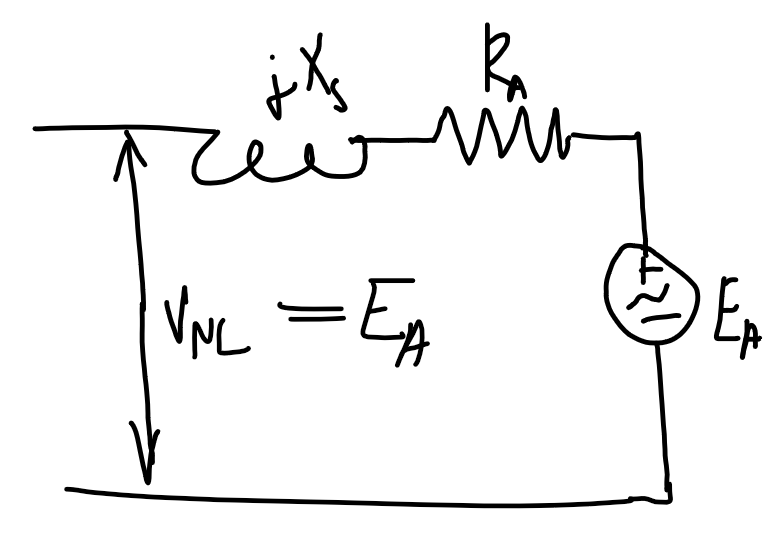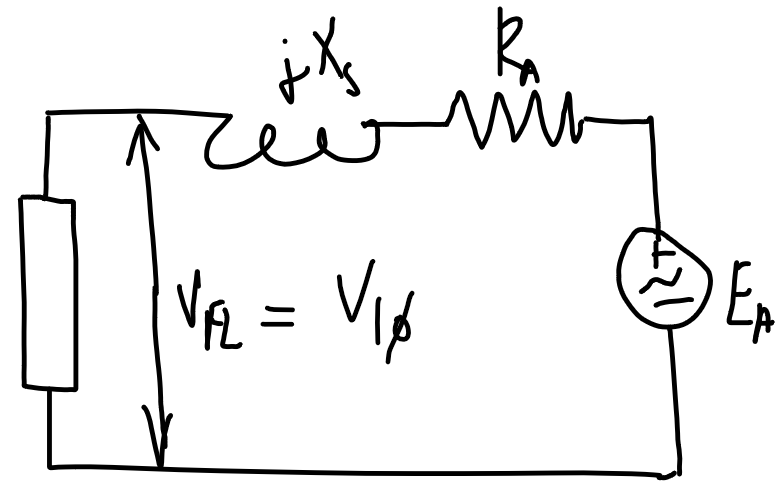Power factor	Voltage regulation
Lagging	Positive
Unity	Near 0
Leading	Negative

Open and short circuit test

Note - double-check if the axis refers to per-phase or line voltage/current.

Open-circuit test	Short-circuit test

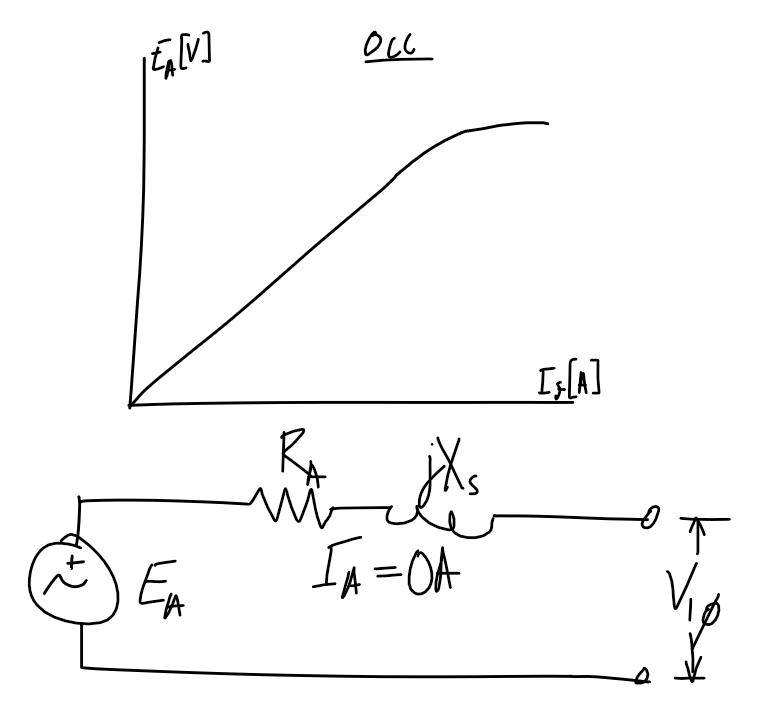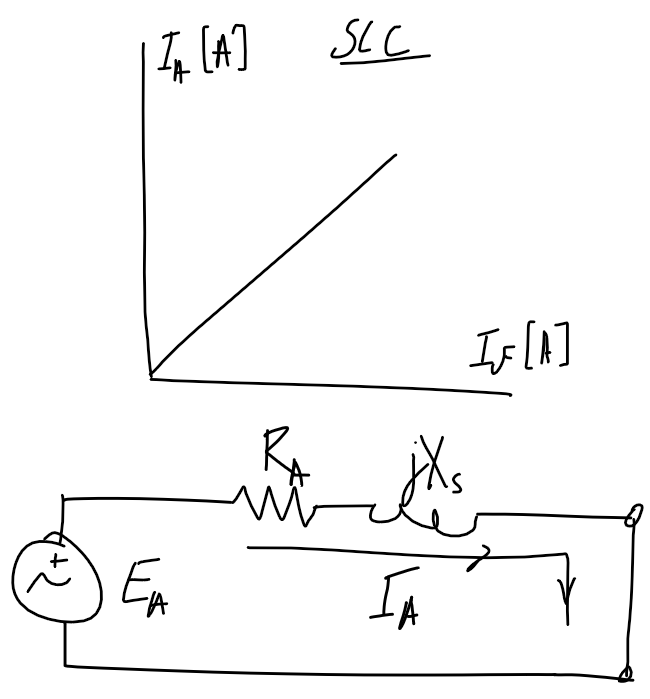Power flow

P_\text{out} is the rated power

P_\text{out}=S_\text{rated}\times \text{PF}

\begin{align}
P_\text{in}&=P_\text{copper}+P_\text{core}+P_\text{F\\\&W}+P_\text{misc}+P_\text{out}\\
P_\text{mech}&=P_\text{F\\\&W}+P_\text{misc}+P_\text{out}
\end{align}

---